Java 中的浮点数相加顺序不同造成结果不同

最近在工作中遇到一个有趣的问题，有个组的同学把代码提交到代码仓库，CI 运行单元测试总是失败。在本地运行又是没有问题的。于是就帮他们找一下原因。其中失败的代码是一段求和后比较结果的代码。 CI 是在 k8s 中运行的。所以我用 docker 在本地使用相同镜像，模拟容器运行环境，发现也不能通过。好事，可以在本地复现，方便调试。

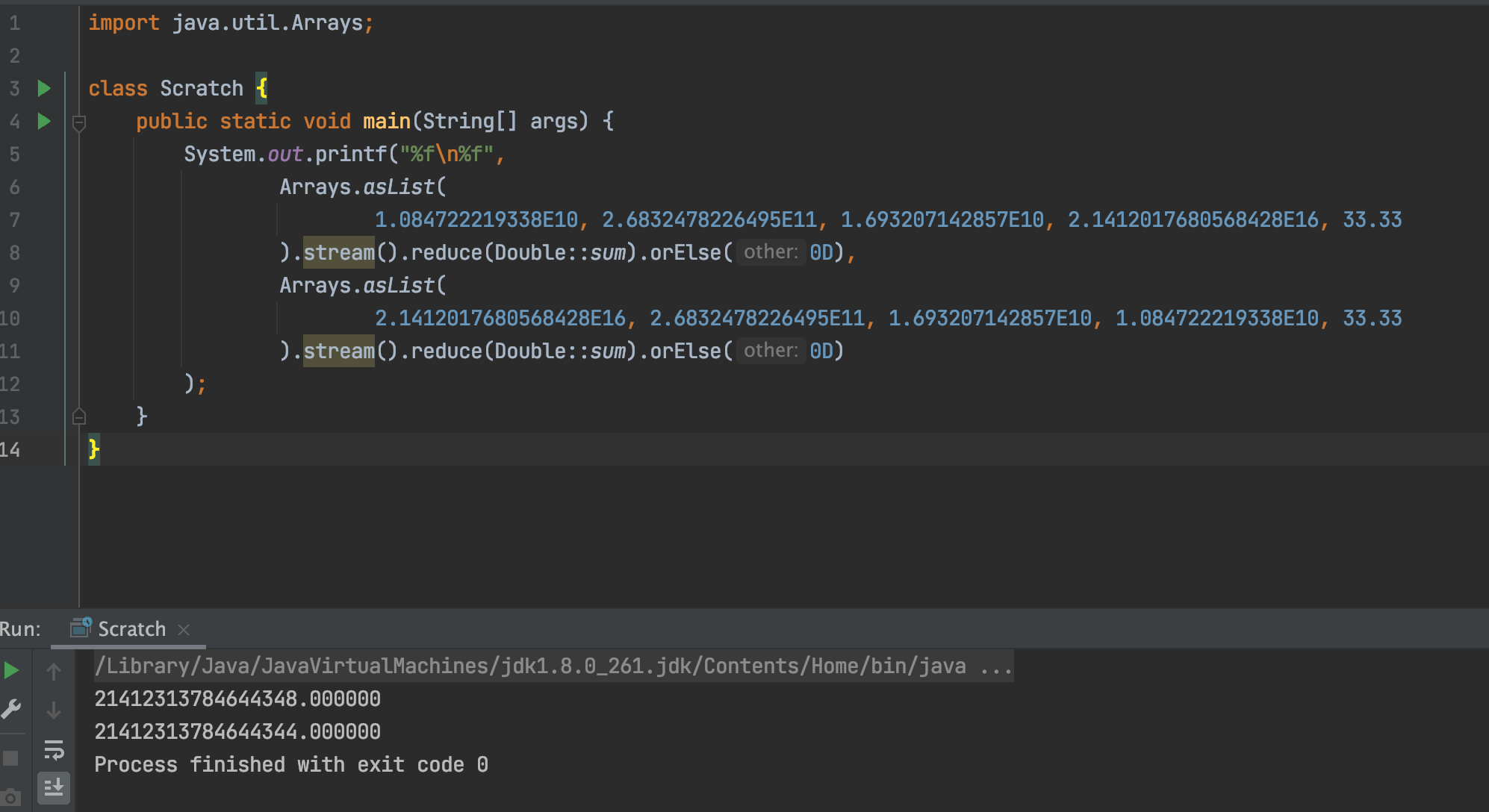
加了一些调试日志，最终把问题定位在几个 double 类型数求和的结果上。容器内运行时，几个数求和的结果和我在本机电脑上求和出来相差 4。仔细对比了每一个数是否一致，确实都是一样的。但结果就是不一样。把几个数放到自己电脑计算一遍。与测试用例中的结果不一样。唯一的区别就是求和时候的顺序不一样。如下面这张图。

为什么浮点数不精确

我们都知道浮点数是不精确的。为什么不精确呢？是所有的浮点数都是不精确的吗？

想要回答这个问题，我们先需要了解一下浮点数是如何被存储在计算机中的。

浮点类型存储结构

先简单回顾一下，Java 中的浮点数存储遵循 IEEE 754 标准。

单精度类型存储结构：

双精度类型存储结构：

IEEE 754 将浮点型数字存储分为 3 部分：

符号域（记录该数字正负）
指数域（记录尾数位偏移）
尾数域（记录数字值）

浮点数的实际值，等于符号位（sign bit）乘以指数偏移值(exponent bias)再乘以分数值(fraction)。

溢出

什么时候会溢出呢？就是当浮点数的长度超过尾数域长度时，精度就会丢失。我们先不考虑小数部分，正整数什么时候会丢失精度。double 类型尾数值是 52 位。最大可以表示 2^52 - 1。但是尾数域还默认最开始有个 1。所以最大可以表示的数为 2^53 - 1

2^53 二进制表示， 10...0 后面 53 个 0。此时因为最后丢弃的一位是 0，其实精度并没有丢失。但我们再加 1，我们看看值会是多少。

class Scratch {
    public static void main(String[] args) {
        double a = 9007199254740992d; // 1<<53
        System.out.printf("%f\n", a-1);
        System.out.printf("%f\n", a);
        System.out.printf("%f\n", a+1);  // 丢失精度
        System.out.printf("%f\n", a+2);
    }
}

输出结果为：

9007199254740991.000000  // 最后一位 1 还在
9007199254740992.000000
9007199254740992.000000  // 最后一位 1 丢失
9007199254740994.000000

第三行输出，因为 2 进制最后一位 1 丢失，所以 a+1 并没有等于 9007199254740993.000000。

溢出浮点数相加顺序造成结果不一致

当我们直接拿一个正常的数 b 与溢出的浮点数 a 相加，无论是 a + b 还是 b + a 结果都是一样的。

class Scratch {
    public static void main(String[] args) {
        double a = 2.1412017680568428E16;
        double b = 279172004458.330000;

        double c = 1.084722219338E10;
        double d = 2.6832478226495E11;

        System.out.printf("%f\n", a + b);
        System.out.printf("%f\n", b + a);
        System.out.println("-------");
        System.out.printf("%f\n", a + c + d);
        System.out.printf("%f\n", c + d + a);

    }
}

输出结果如下：

21412296852572888.000000
21412296852572888.000000
-------
21412296852572884.000000
21412296852572888.000000

a 的二进制表示为 1001100000100100001110111011011110001100101000001101100, 有 55 位，尾数的值为 0011000001001000011101110110111100011001010000011011，最后两位丢失。

a + c 时，c 的整数位最后两位被舍弃了。再加 d 时，d 的最后两位又舍弃了。但是 c + d 的结果，再加 a 时，最后两位进了一位，相当于再原来舍弃的基础上加了 4（二进制 100）。这就是为什么最终两次计算结果相差 4。而这个取舍规则，有机会再单独写一篇。

总结

由于一次浮点数不同顺序相加造成不同结果，复习了浮点数是如何存储，解释了为什么浮点数会不精确，以及找到了最终为什么最初两次不同顺序的 double 类型数相加结果相差 4。

Eirture

Java 中的浮点数相加顺序不同造成结果不同

为什么浮点数不精确

浮点类型存储结构

溢出

溢出浮点数相加顺序造成结果不一致

总结

参考